6.2. Paraboloide
La parábola y la hipérbole tienen su correspondencia tridimensional en los llamados paraboloides. Una parábola en revolución, girando sobre su eje de simetría, crea un paraboloide elíptico. Una superficie tridimensional que tiene la propiedad de reflejar hacia su foco, como la parábola, los rayos paralelos entrantes en todos sus puntos. Imaginemos una de las antenas parabólicas instaladas en tantos tejados: son paraboloides de revolución, que conservan las propiedades de la parábola. Cada punto de la superficie refleja en su foco, donde se instala el brazo con el receptor de la señal, las ondas paralelas que impactan sobre él.
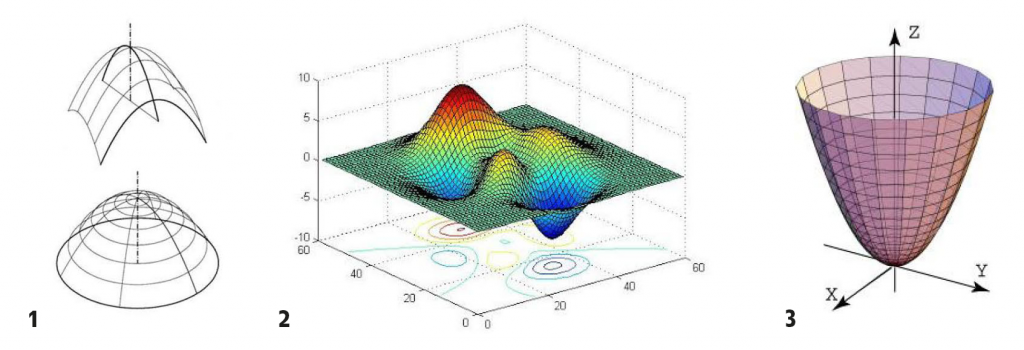
2. Superficies parabólicas que nos recuerdan orografías. Imagen disponible en: http://www.vc.ehu.es/campus/centros/farmacia/deptos-f/depme/apuntes/gracia/Curso_Actual/OCW/Matematicas_Calc_Dife_EDO.htm. [Fecha de consulta: 18.03.20].
3. Otra expresión del paraboloide elíptico. Imagen disponible en: http://www2.udec.cl/~juanerodriguez/s4.html. [Fecha de consulta: 18.03.20].
1) Por un lado, el paraboloide hiperbólico. Si nos fijamos en una de sus secciones, veremos dos parábolas, una hacia arriba y otra hacia abajo. Si nos fijamos en la sección perpendicular a la anterior, veremos una hipérbola. El paraboloide hiperbólico genera la famosa forma de la silla de montar o un plano alabeado o combado, ejemplo muy visual de lo que es un paraboloide hiperbólico. Sin embargo, lo podemos encontrar, como veremos, en muchas estructuras de la naturaleza.
2) Por otro lado, la revolución de una hipérbola genera lo que se denomina un hiperboloide, figura que se entiende muy bien visualmente. Viene a ser el giro completo sobre sí misma y puede generar un volumen de una o de dos hojas.

2 Paraboloide hiperbólico diseñado por el arquitecto Frei Otto, Music Pavillion, 1955. Imagen disponible en: https://es-la.facebook.com/MilanoDesignFilmFestival/photos/a.204231873072581/738884096274020/?type=3&theater. [Fecha de consulta: 18.03.20].
3. Forma de paraboloide en “silla de montar”. Imagen disponible en: https://es.wikipedia.org/wiki/Paraboloide. [Fecha de consulta: 18.03.20].