6.1. La parábola
Un cono es un gran generador de formas. Como figura geométrica, es un sólido de revolución generado por una recta llamada generatriz que gira «pivotando» sobre un punto fijo: el vértice del cono. También lo podemos imaginar como un triángulo rectángulo girando sobre sí mismo: uno de los catetos nos da la altura, el otro el radio de la base, mientras que la hipotenusa sería la recta generatriz.
Llamamos curvas cónicas a las que están formadas por la intersección de un plano con un cono. Cuando el plano es paralelo a la base del cono, obtenemos una circunferencia. Si el plano es oblicuo a la base del cono, el resultado es una elipse. La hipérbola la obtenemos cuando el plano corta el cono perpendicularmente a la base. Si el plano corta el cono entre la dirección perpendicular a la base y la recta generatriz, obtendremos una parábola. La parábola se enmarca en las denominadas curvas cónicas.
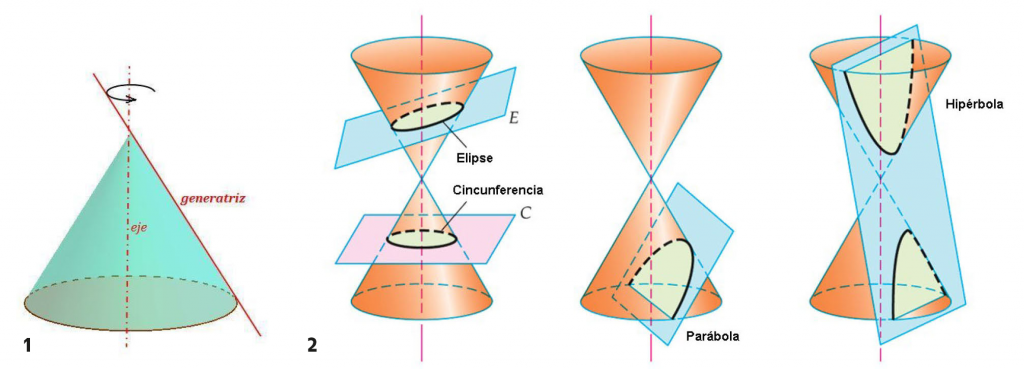
2. Curvas cónicas. Imagen disponible en: http://trigoygeouts.blogspot.com/p/conicas.html. [Fecha de consulta: 18.03.20].
Igual que la circunferencia, la elipse conserva propiedades muy interesantes de equidistancia entre los focos y los puntos de la curva. La suma de las distancias de cualquier punto de la elipse a los dos focos nos dará su eje mayor. Se mantiene una constancia de todos los puntos de la curva respecto de sus focos.
Volviendo a la parábola… Imaginemos que lanzamos un objeto al aire en una dirección de 45 grados respecto el suelo. Ese objeto va a describir una parábola, es decir, un fragmento de elipse, ¡uno de cuyos focos es el centro de la tierra! Ese lanzamiento reproduce a microescala (con algunas variables, claro, como la resistencia del aire) el movimiento elíptico que describen las órbitas planetarias.