6.1. La paràbola
Un con és un gran generador de formes. Com a figura geomètrica, és un sòlid de revolució generat per una recta anomenada generatriu que gira «pivotant» sobre un punt fix: el vèrtex del con. També el podem imaginar com un triangle rectangle girant sobre si mateix: un dels catets ens dona l’altura, l’altre el radi de la base, mentre que la hipotenusa és la recta generatriu.
Anomenem corbes còniques aquelles que estan formades per la intersecció d’un pla amb un con. Quan el pla és paral·lel a la base del con, obtenim una circumferència. Si el pla és oblic a la base del con, el resultat és una el·lipse. La hipèrbola l’obtenim quan el pla talla el con perpendicularment a la base. Si el pla talla el con entre la direcció perpendicular a la base i la recta generatriu, obtenim una paràbola. La paràbola s’emmarca en les denominades corbes còniques.
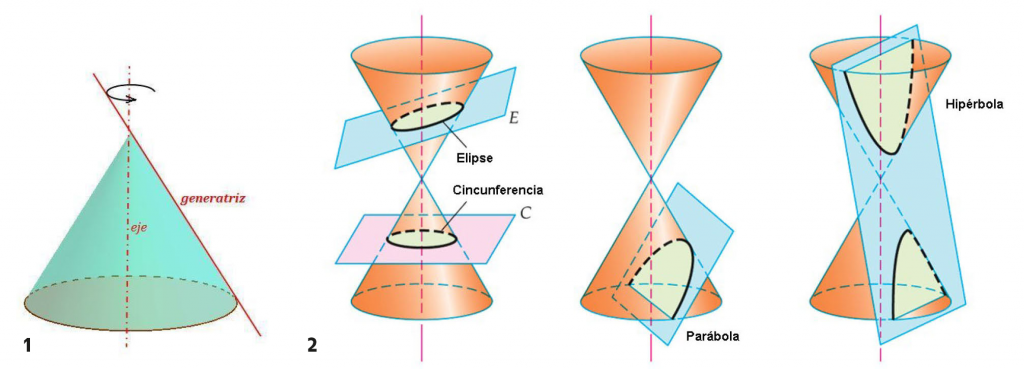
2) Corbes còniques. Imatge disponible a: http://trigoygeouts.blogspot.com/p/conicas.html. [Data de consulta: 18.03.2020].
Igual que la circumferència, l’el·lipse conserva propietats molt interessants d’equidistància entre els focus i els punts de la corba. La suma de les distàncies de qualsevol punt de l’el·lipse als dos focus ens donarà el seu eix major. Es manté una constància de tots els punts de la corba respecte dels seus focus.
Tornant a la paràbola… Imaginem que llancem un objecte a l’aire en una direcció de 45 graus respecte del terra. Aquest objecte descriurà una paràbola, és a dir, un fragment d’el·lipse, un dels focus de la qual és el centre de la Terra! Aquest llançament reprodueix a microescala (amb algunes variables, clar, com la resistència de l’aire) el moviment el·líptic que descriuen les òrbites planetàries.
D’altra banda, de la mateixa manera que tots els punts d’una el·lipse estan en relació amb els seus focus, els punts d’una corba parabòlica també ho estan amb el focus. Qualsevol recta que incideixi en la corba es «reflectirà» passant per aquest punt. El que arriba de l’infinit es concentrarà en el focus. I al revés, tot el que surt d’aquest punt s’envia a l’infinit. Com veurem, aquesta característica ha estat ben aprofitada tant en el món viu com en el món culte.