6.2. Paraboloide
La paràbola i la hipèrbole tenen la seva correspondència tridimensional en els anomenats paraboloides. Una paràbola en revolució, girant sobre el seu eix de simetria, crea un paraboloide el·líptic, una superfície tridimensional que té la propietat de reflectir cap al seu focus, com la paràbola, els raigs paral·lels entrants en tots els seus punts. Imaginem una de les antenes parabòliques instal·lades en tantes teulades: són paraboloides de revolució, que conserven les propietats de la paràbola. Cada punt de la superfície reflexa en el seu focus, on s’instal·la el braç amb el receptor del senyal, les ones paral·leles que impacten sobre ell.
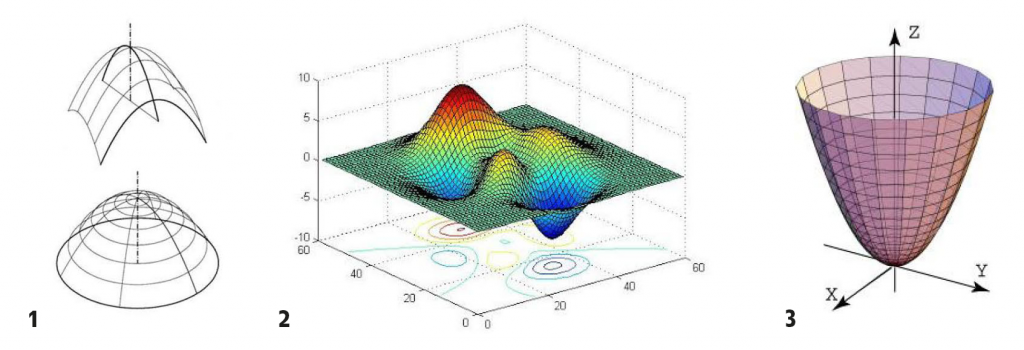
2) Superfícies parabòliques que ens recorden orografies. Imatge disponible a: http://www.vc.ehu.es/campus/centros/farmacia/deptos-f/depme/apuntes/gracia/curso_actual/ocw/matematicas_calc_dife_edo.html. [Data de consulta: 18.03.2020].
3) Una altra expressió del paraboloide el·líptic. Imatge disponible a: http://www2.udec.cl/~juanerodriguez/s4.html. [Data de consulta: 18.03.2020].
1) D’una banda, el paraboloide hiperbòlic. Si ens fixem en una de les seves seccions, veurem dues paràboles, una cap amunt i una altra cap avall. Si ens fixem en la secció perpendicular a l’anterior, veurem una hipèrbola. El paraboloide hiperbòlic genera la famosa forma de la cadira de muntar o un pla guerxo o blegat, exemple molt visual del que és un paraboloide hiperbòlic. No obstant això, el podem trobar, com veurem, en moltes estructures de la naturalesa.
2) D’altra banda, la revolució d’una hipèrbola genera el que es denomina un hiperboloide, figura que s’entén molt bé visualment. Ve a ser el gir complet sobre si mateixa i pot generar un volum d’una fulla o de dues.

2) Paraboloide hiperbòlic dissenyat per l’arquitecte Frei Otto, Music Pavillion, 1955. Imatge disponible a: https://es-la.facebook.com/milanodesignfilmfestival/photos/a.204231873072581/738884096274020/?type=3&theater. [Data de consulta: 18.03.2020].
3) Forma de paraboloide en «cadira de muntar». Imatge disponible a: https://es.wikipedia.org/wiki/paraboloide. [Data de consulta: 18.03.2020].