7.4. Els fractals en el món culte
El concepte matemàtic de fractal es consolida amb Mandelbrot, en un moment molt propici per al seu desenvolupament gràcies a la incipient indústria de la computació, la fabricació de màquines per a iterar patrons a grans velocitats: des dels sistemes de funcions iterades (iterated function systems o IFS) que John E. Hutchinson va començar a fer el 1981, els quals reprodueixen «senzills» fractals autosemblants, fins als actuals gràfics de Pixar, fets sobre la base de complexes estructures geomètriques generades a partir de fractals.
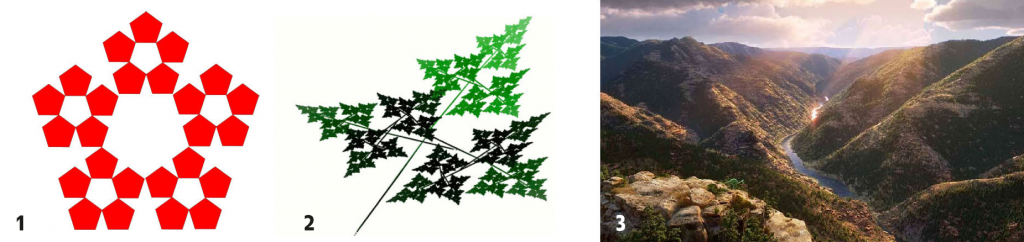
2) Fractals. Imatge disponible a: http://www3.gobiernodecanarias.org/medusa/ecoblog/mrodperv/fractales/fractales-generados-por-ifs. [Data de consulta: 12.03.2020].
3) Fotograma d’una pel·lícula d’animació. Imatge disponible a: http://mimamatieneunblog.com/como-pelicula-animacion-pixar. [Data de consulta: 12.03.2020].
Recapitulem. Les formes fractals tendeixen a distribuir-se uniformement per l’espai, maximitzen l’entropia de forma, distribuint-se a l’atzar amb un màxim d’uniformitat. Doncs bé, això ho podem aplicar tant a l’anàlisi de moviments borsaris com als quadres de Pollock, així com a molts patrons que es generen en xarxa i que constitueixen la xarxa mateixa (www). De fet, i com a curiositat, R. Taylor, A. Micolich i D. Jonas, científics australians, van arribar a mesurar la dimensió fractal dels quadres de Pollock, i així van arribar fins i tot a determinar-ne l’autenticitat i la data. Sembla que la seva pintura va arribar a ser veritablement fractal a partir de 1942, en què va prendre valors superiors a 1 i va augmentar progressivament la seva fractalitat fins el 1952.

2) La pintura de Pollock i la seva dimensió fractal. Imatge disponible a: https://www.xatakaciencia.com/matematicas/los-fractales-en-la-pintura-de-pollock. [Data de consulta: 12.03.2020].
3) Representació gràfica dels ISP i nodes d’internet. Imatge disponible a: http://informatica.blogs.uoc.edu/2012/11/12/la-belleza-de-las-redes-herramientas-de-visualizacion-de-grafos. [Data de consulta: 12.03.2020].